Explaining Scala’s `val` function syntax

This is an excerpt from my book on Functional Programming in Scala. It’s an appendix that “explains and explores” Scala’s function syntax.

Background

I wrote in the “Functions are Values” lesson that most developers prefer to use the def syntax to define methods — as opposed to writing functions using val — because they find the method syntax easier to read than the function syntax. When you write methods, you let the compiler convert them into functions with its built-in “Eta Expansion” capability. There’s nothing wrong with this. Speaking as someone who used Java for 15+ years, the def syntax was easier for me to read at first, and I still use it a lot.

But if you come from something like a Haskell background, you may find that the val function syntax is easier to read; it’s more familiar. Or, once you dig into the val function syntax — as shown in this lesson — you may say, “Hey, I prefer the val syntax.”

Beyond your background and preferences, there’s another important point about val functions: You’ll use the exact same syntax to define functions as input parameters. For example, this calculate function declares an input parameter named f:

calculate(f: (Int, Int) => Int)

f is a function that transforms two Int values into a resulting Int value, and the syntax you use to define f’s type is the same syntax that I explore in this lesson.

Goals

Given that background, the primary goal of this lesson is to explain and demonstrate Scala’s val syntax for writing functions. I’ll show both forms of the function syntax, (a) the “explicit return type” syntax, and (b) the “implicit return type”  syntax.

I also show that when you define a function as a val, what you’re really doing is giving a value name to an anonymous function. Finally, I also show that behind the scenes, when Scala compiles a function, what it really does is create an instance of the Function0 through Function22 traits.

Scala’s function syntax

In Scala, there are at least two syntax forms for defining functions using val. The biggest distinction is whether you want to (a) let the return type be “implicit” — meaning that you don’t show it, and the compiler infers it — or (b) define the function’s return type explicitly.

In this lesson I’m going to use the terms “explicit return type” (ERT), and “implicit return type” (IRT). These aren’t industry-standard acronyms, but because I will be using these phrases often in this lesson, I have come up with these acronyms.

The following lines show the implicit and explicit syntax for a function named add1, which returns an Int value that is 1 larger than the Int value it is given as an input parameter:

val add1 = (i: Int) => i + 1           // implicit return type (IRT)
val add1: Int => Int = (i) => i + 1    // explicit return type (ERT)

One variation of this is that you can put curly braces around the function body:

val add1 = (i: Int) => { i + 1 }
val add1: Int => Int = (i) => { i + 1 }

You generally need to use curly braces around multi-line functions, but you can also use them in one-line functions if you prefer.

With the ERT syntax, when you have only one input parameter, you can leave the parentheses off of the parameter name:

val add1: Int => Int = (i) => { i + 1 }
val add1: Int => Int =  i  => { i + 1 }   // parentheses not required

All of those examples show a function that takes one input parameter. The next examples show the syntax for a sum function that takes two input parameters:

val sum = (a: Int, b: Int) => a + b            // implicit
val sum: (Int, Int) => Int = (a, b) => a + b   // explicit

When I first came to Scala from Java, I didn’t like this syntax — at all — but now that I understand it, I have no problems with it, and even like it.

Explaining the ERT syntax

This image explains the fields in the ERT version of the sum function:

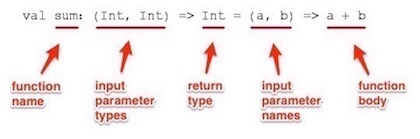
As that shows, the signature consists of:

• Assigning a function name, sum.
• The function’s input parameter type(s).
• The function’s return type.
• Giving names to the function’s input parameters.
• Writing the function body.

In any programming language that declares its input and output types, you need to declare all of these things; it’s just a matter of how you declare them that makes each approach different. For instance, when you look at Scala’s method syntax, you see that it requires the exact same fields, they’re just ordered differently, with different field-separator symbols:

def sum(a: Int, b: Int): Int = a + b

Viewing the function signature as two blocks

A way that really helped me understand the function syntax was to break it up into different “blocks.” If you look at the signature as two blocks, like this:

you can see that the first block declares the function’s input and return types:

If you’ve worked with a language like C, where you declare a function’s types in a header file, this becomes clear.

In a similar manner, the second block declares the function’s input parameter names and the function’s algorithm:

A key point of this block is that it shows how the input parameter names are used within the algorithm; it makes sense that the parameter names are close to the function body.

I find that when I highlight the code like this, the val function signature makes a lot of sense.

=>, the “Universal Transformer”

Furthermore, because I like to think of the => symbol as Scala’s “Universal Transformer” – like Star Trek’s “Universal Translator” — I can also look inside each block to see the intended transformation.

For instance, the => symbol in the first block of the sum function shows that it transforms two input Int values into an Int return value:

The => in the second block similarly shows how the function transforms its input parameter names with its algorithm:

Reading IRT function signatures

Those examples show how you can read the function signature when you explictly show the function’s return type, i.e., the ERT approach. You can use a similar approach to understand the implicit return type syntax.

To demonstrate this, the following isEven function determines whether the input Int parameter is an even or odd number. It returns a Boolean value, but because you and the Scala compiler can both infer the return type by looking at the function body, I don’t explicitly declare it:

val isEven = (i: Int) => i % 2 == 0

You can view the fields in isEven like this:

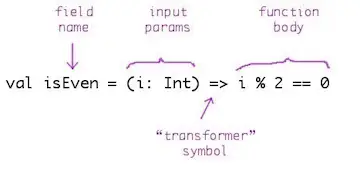
As with the previous examples, you can see in the signature that the “Universal Transformer” symbol transforms an input value to an output value:

This IRT syntax is more concise than the ERT syntax, and it’s similar to the def method signature.

With both the ERT and IRT signatures, I find that it helps to read function signatures as sentences. Fo example, I read this function:

val isEven = (i: Int) => i % 2 == 0

like this:

“The function isEven transforms the input Int into a Boolean value based on its algorithm, which in this case is i % 2 == 0.”

Exercise

• Take a moment to sketch the syntax for an isEven function that declares an explicit return type:

Key: Using return doesn’t feel right

Another eye-opener for me is that once I understood the val function syntax, I realized that using Scala’s return keyword doesn’t feel right. To me, this code looks and feels right:

val isEven = (i: Int) => i % 2 == 0

But this attempt to use return does not look right:

val isEven = (i: Int) => return i % 2 == 0

With the function syntax you’re not really “returning” anything, you’re just assigning a block of code to a value, so return feels out of place here. (In fact, return is so out of place here that the second example won’t even compile.)

There are times I still want to “return” something from a def method, but I find that I never want to use return when I use the val function syntax. As I wrote in the early “Functional Code Feels Like Algebra” lesson, in FP you really are writing a series of equations.

Examples of function syntax using isEven

If the body of isEven (i % 2 == 0) is hard to read, that’s okay, for at least one reason: It gives me a chance to write a little more about the function syntax.

First off, it may help to know that the isEven function I showed originally:

val isEven = (i: Int) => i % 2 == 0

is a shorthand way of writing this:

val isEven = (i: Int) => if (i % 2 == 0) true else false

This longer form makes it more clear about how isEven works. If you really prefer longer forms, you can write this same function like this:

val isEven = (i: Int) => {
    if (i % 2 == 0) {
        true
    } else {
        false
    }
}

I show these examples because I want to list the many ways you can write isEven using an implicit return type:

val isEven = (i: Int) => { if (i % 2 == 0) true else false }
val isEven = (i: Int) => if (i % 2 == 0) true else false

val isEven = (i: Int) => { i % 2 == 0 }
val isEven = (i: Int) => i % 2 == 0
val isEven = i: Int => i % 2 == 0

The next examples show different ways you can write isEven when declaring an explicit return type:

val isEven: (Int) => Int = (i) => { if (i % 2 == 0) true else false }
val isEven: (Int) => Int = i   => { if (i % 2 == 0) true else false }

val isEven: (Int) => Int = (i) => { i % 2 == 0 }
val isEven: (Int) => Int = i   => { i % 2 == 0 }

val isEven: (Int) => Int = (i) => i % 2 == 0
val isEven: (Int) => Int = i   => i % 2 == 0

val isEven: (Int) => Int = (i) => {
    if (i % 2 == 0) {
        true
    } else {
        false
    }
}

There are even more ways that you can write isEven. Later in this lesson I’ll show how you can write it by explicitly extend Function1 with the anonymous class syntax.

The REPL shows the explicit function syntax

It’s interesting to note that the REPL shows the same function signature whether I use the ERT or IRT syntax:

// ERT
scala> val sum: (Int, Int) => Int = (a, b) => a + b
sum: (Int, Int) => Int = <function2>

// IRT
scala> val sum = (a: Int, b: Int) => a + b
sum: (Int, Int) => Int = <function2>

But what I really like about the REPL output is that it shows the ERT function syntax. Note the similarity between the ERT syntax I wrote, and what the REPL responds with:

val sum: (Int, Int) => Int = (a, b) => a + b    // my code
    sum: (Int, Int) => Int = <function2>        // repl output

The type signature the REPL shows is identical to the ERT’s type signature.

We’re giving an anonymous function a name

Assuming that you’ve already written anonymous functions in Scala, you may have noticed that what I’m doing in all of these examples is that I’m assigning the anonymous function i % 2 == 0 to a val named isEven:

val isEven = (i: Int) => i % 2 == 0

What I mean by that is that this code is an anonymous function:

             (i: Int) => i % 2 == 0

and the only thing the previous code is doing is assigning the value named isEven to this anonymous function. You can see that more clearly in these images. First, the anonymous function part:

Then the value being assigned to the anonymous function:

As another way of showing this, you can paste the anonymous function into the REPL:

scala> (i: Int) => i % 2 == 0
res0: Int => Boolean = <function1>

and then assign isEven to res0:

scala> val isEven = res0
isEven: Int => Boolean = <function1>

After that, you can use isEven as before:

scala> isEven(42)
res1: Boolean = true

As shown, the function syntax just assigns a value name to an anonymous function.

isEven is an instance of Function1

I discuss this next point in the “Functions are Values” lesson, so I won’t go into it too much here, but it’s worth mentioning that in all of these examples, isEven is an instance of the Function1 trait.

This is what the output is trying to tell you when you paste isEven into the REPL:

scala> val isEven = (i: Int) => i % 2 == 0
isEven: Int => Boolean = <function1>

The REPL output shows that isEven’s result is an instance of Function1, which it shows as <function1>.

If you haven’t seen this before, the reason that isEven is an instance of Function1 is because it takes one input parameter. The Function1 Scaladoc shows that this is exactly what it’s intended for:

By comparison, a sum function that takes two input parameters is an instance of the Function2 trait:

scala> val sum: (Int, Int) => Int = (a, b) => a + b
sum: (Int, Int) => Int = <function2>

In fact, I note in “The differences between def and val when defining functions” appendix that, if you want to, you can define sum like this:

val sum = new Function2[Int, Int, Int] {
    def apply(a: Int, b: Int): Int = a + b
}

As I show in that appendix, that’s what the Scala compiler really does for you when you define sum.

Finally, while I’m in the neighborhood, this is how you define isEven using this approach:

val isEven = new Function1[Int, Boolean] {
    def apply(i: Int): Boolean = i % 2 == 0
}

Most developers don’t use this approach; I’m just trying to show how things work under the hood.

Conspiracy Theory: The function syntax has its root in Haskell

I can neither confirm nor deny what I’m about to write, but in the spirit of a good The X-Files conspiracy, I suspect that this syntax:

val sum: (Int, Int) => Int = (a, b) => a + b

has its roots in Haskell, or perhaps another language like ML (which I only know from looking at its Wikipedia page).

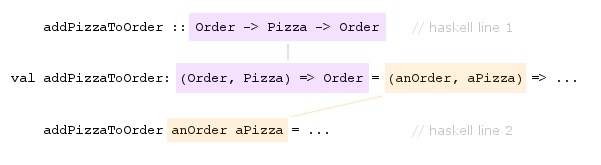
The reason I suspect this is because of how you define Haskell functions. For example, here’s the Haskell syntax to define a function named addPizzaToOrder, which takes Order and Pizza instances as input parameters, and returns a new Order as a result:

addPizzaToOrder :: Order -> Pizza -> Order
addPizzaToOrder anOrder aPizza = (function body here ...)

The first line shows the function’s signature, which includes only (a) the function name, (b) its input types, and (c) its output type. This is a little like declaring a function signature in a C header file.

In Haskell, it’s a slight simplification to say that the output type is the last type listed after the string of -> symbols. So in this example, the addPizzaToOrder function returns an Order.

The second line shows the input parameter names (anOrder, aPizza), which correspond to the types declared on the first line (Order, Pizza). The same function is written like this using Scala’s ERT syntax:

val addPizzaToOrder: (Order, Pizza) => Order = (anOrder, aPizza) => ???

I don’t know about you, but to me it looks like the Scala syntax merges the two Haskell lines into one line:

But again, this is just X-Files speculation. I’ve never spoken to Martin Odersky or anyone else about this. ;)

(As supporting conspiracy theory material, Haskell 1.0 was defined in 1990, and the “Haskell 98” standard was published in February, 1999. The history of Scala on Wikipedia states, “The design of Scala started in 2001 ... following from work on Funnel, a programming language combining ideas from functional programming and Petri nets. After an internal release in late 2003, Scala 1.0 was released publicly in early 2004 on the Java platform.” So, the timeline fits the conspiracy theory. ;)

For more information on Scala’s history, see Scala’s Prehistory on scala-lang.org.

Summary

The intent of this lesson was to explain and explore Scala’s function syntax. Here’s a summary of what was covered:

• I showed two forms of the Scala function syntax, showing the implicit return type (IRT) syntax, and the explicit return type (ERT) syntax.
• I showed how you can break the ERT syntax down into blocks to understand it more easily.
• I showed that the REPL output for functions looks just like the ERT type signature syntax.
• I showed where the => (Universal Transformer) symbol fits in both the ERT and IRT approaches.
• I noted that since the function approach really just assigns a block of code to a val field, it doesn’t feel right to use the return keyword when defining functions.
• I noted that all we’re really doing when we define a function is giving a name to an anonymous function.
• I showed that “under the hood,” you’ll find that functions are instances of traits like Function1 and Function2.
• Then I took a detour and shared a little conspiracy theory. ;)

See also

• Scala’s Function1 trait
• The ML programming language
• The Funnel programming language
• history of Scala on Wikipedia
• Scala’s Prehistory on scala-lang.org