Pure Functions Cannot Lie (Scala 3 Video)

JIT: I Love Pure Functions, They Cannot Lie

I initially thought that pure functions were “nice,” but when I really started using them I thought, wow, this is important: input goes in front door, and output comes out the back door, as shown in this first image:

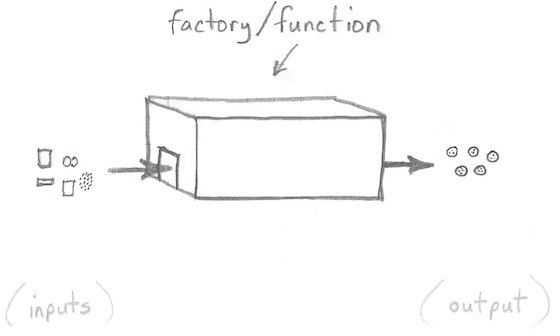
Very importantly, there are no side doors for side effects (bad things) to sneak in and out:

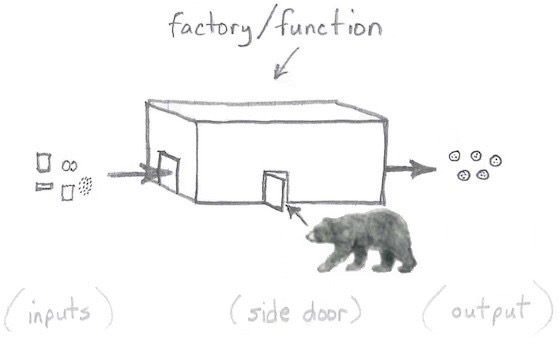
Pure functions do not lie

My overwhelming thought was, “Whoa, I can look ONLY at the signature of a pure function to know what it does.” No more digging into the source code of impure methods; just look at the function signature.

This hit me so hard that I immediately wanted to write an impure annotation to mark all those old methods I had written as being impure:

@impure
def randomInt(): Int = scala.util.Random.nextInt

I knew this wasn’t a proper solution — because I had no way to enforce the annotation — but I REALLY wanted a way to tell the pure from the impure just by looking at function signatures.

As you’ll come to see in the remainder of this book, you can easily tell that this particular function is impure because it takes no input parameters. Any time you see a function with no input parameters, it’s a clear sign that a side effect is happening inside that function.

Pure functions reduce your cognitive load

Not to gush too much, but I LOVE writing pure functions: they make things MUCH easier on my brain.

What I mean is that when I write a pure function, I don’t have to think about the rest of the application. When I write a pure function, my entire universe — the only things I need to think about — are:

• What input parameters do I need?
• What is my pure function’s return type?
• What is its algorithm?

Literally, the only thing in my mind when I’m writing a pure function looks like this:

                            +------------+
(p1: Type1, p2: Type2)  =>  |  function  |  =>  result: ResultType
----------------------      +------------+      -------------------
   Input Parameters                             The Function Result

There’s no need to worry about mutating the variables I’m given, or variables in the class or available globally. I just think about (a) what comes in, (b) what goes out, and (c) the function’s algorithm.

Once I realized this, even the imposter syndrome in me thought, “You know, I don’t know if I can think about an entire application today. But I can certainly write one pure function. And then I can write another. And another. And then eventually I can glue them together to solve bigger problems.”

As you’ll see in this book, glueing pure functions together is also just like algebra.

One other thing: I also found that I like reading the signatures of pure functions that other people write. Unlike OOP-style methods that can return void and/or take no input parameters — which makes their type signatures meaningless — when I look at the type signature of a pure function, I can tell at a glance what’s going on.

Another pop quiz

Here’s another little quiz: Knowing that this function is pure, what can it possible do:

def f(list: List[Int]): Int = ???

If you’re new to Scala, this code defines a function that takes a list of integers as input, and returns an integer as its result:

• def f tells you that it’s a function named f.
• It takes an input parameter that I have named list, and its type is List[Int], meaning that it is a sequence (list) of integers.
• The function returns an integer (Int).

I encourage you to write down everything you think that pure function can possibly do.

As a second question, here’s the same function signature, but with a generic type. Again, what can it possibly do:

def g[A](list: List[A]): A = ???

If you’re not familiar with generic types, this just means that this function can take a list of integers (List[Int]), a list of strings (List[String]), a list of people (List[Person]), etc. The data type inside the List doesn’t matter to the algorithm; the algorithm must only concern itself with the fact that it’s given a list.

The A as the return type means that the function returns a single element that is the same data type that’s contained inside the list. So if the function receives a (List[Int]) as input, it must return an Int; and if it gets a (List[Person]), it must return a Person, etc.

Again, I encourage you to write down everything you think this function can possibly do.

Key points

As a summary, there are several key points from these last two chapters:

• Pure functions reduce your cognitive load. When you’re writing them, all you have to think about is their input, output, and algorithm.
• You can trust pure functions, they cannot lie. Their signatures tell you exactly what they can (and cannot) do.

Also — I’ll repeat this many times in this book — but writing code using pure functions (and immutable things) feels just like writing algebra. You start by writing a few pure functions like this:

def add(i: Int, j: Int): Int
def multiply(i: Int, j: Int): Int

and then you glue them together like this:

val x = add(1, 1)
val y = multiply(x, 2)

or this:

val z = multiply(add(1, 1), 2)

Or, if you like architecture and engineering, this style of programming is just like creating a blueprint. You’re connecting pipes and wires together, and because pure functions can’t throw exceptions, all these pipes and beams “just connect” to each other. (You don’t have to worry about functions throwing exceptions and blowing up your design.)