A Visual Look at Java/JVM Stacks and Frames

Given the background information of the previous lesson, let’s take a visual look at how the Java/JVM stack and stack frames work by going back to our recursive sum function from the previous lesson.

The Java/JVM call stack

Before the sum function is initially called, the only thing on the call stack is the application’s main method:

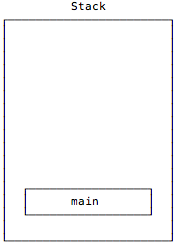
Then main calls sum with List(1,2,3), which I show here without the “List” to keep things simple:

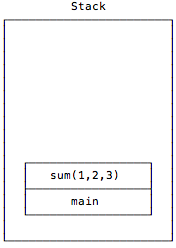
The data that’s given to sum matches its second case expression, and in my pseudocode, that expression evaluates to this:

return 1 + sum(2,3)

Next, when a new instance of sum is called with List(2,3), the stack looks like this:

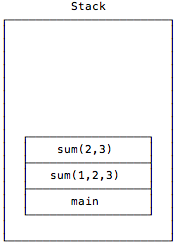
Again the second case expression is matched inside of sum, and it evaluates to this:

return 2 + sum(3)

When a new instance of sum is called with the input parameter List(3), the stack looks like this:

Again the second case expression is matched, and that code evaluates to this:

return 3 + sum(Nil)

Finally, another instance of sum is called with the input parameter List() — also known as Nil — and the stack now looks like this:

This time, when sum(Nil) is called, the first case expression is matched:

case Nil => 0

That pattern match causes this sum instance to return 0, and when it does, the call stack unwinds and the stack frames are popped off of the stack, as shown in this series of images:

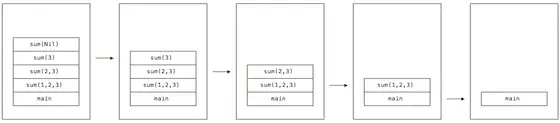
In this process, as each sum call returns, its frame is popped off of the stack, and when the recursion completely ends, the main method is the only frame left on the call stack. (The value 6 is also returned by the first sum invocation to the place where it was called in the main method.)

I hope that gives you a good idea of how recursive function calls are pushed-on and popped-off the JVM call stack.

Manually dumping the stack with the sum example

If you want to explore this in code, you can also see the series of sum stack calls by modifying the sum function. To do this, add a couple of lines of code to the Nil case to print out stack trace information when that case is reached:

def sum(list: List[Int]): Int = list match {
    case Nil => {
        // this manually creates a stack trace
        val stackTraceAsArray = Thread.currentThread.getStackTrace
        stackTraceAsArray.foreach(println)
        // return 0 as before
        0
    }
    case x :: xs => x + sum(xs)
}

Now, if you call sum with a list that goes from 1 to 5:

val list = List.range(1, 5)
sum(list)

you’ll get this output when the Nil case is reached:

java.lang.Thread.getStackTrace(Thread.java:1588)
recursion.SumWithStackDump$.sum(SumWithStackDump.scala:19)
recursion.SumWithStackDump$.sum(SumWithStackDump.scala:19)
recursion.SumWithStackDump$.sum(SumWithStackDump.scala:19)
recursion.SumWithStackDump$.sum(SumWithStackDump.scala:19)
recursion.SumWithStackDump$.sum(SumWithStackDump.scala:19)

While that output isn’t too exciting, it shows that when the stack dump is manually triggered when the Nil case is reached, the sum function is on the stack five times. You can verify that this is correct by repeating the test with a List that has three elements, in which case you’ll see the sum function referenced only three times in the output:

java.lang.Thread.getStackTrace(Thread.java:1588)
recursion.SumWithStackDump$.sum(SumWithStackDump.scala:13)
recursion.SumWithStackDump$.sum(SumWithStackDump.scala:19)
recursion.SumWithStackDump$.sum(SumWithStackDump.scala:19)

Clearly the sum function is being added to the stack over and over again, once for each call.

I encourage you to try this on your own to become comfortable with what’s happening.

Summary: Our current problem with “basic recursion”

I hope this little dive into the JVM stack and stack frames helps to explain our current problem with “basic recursion.” As mentioned, if I try to pass a List with 10,000 elements into the current recursive sum function, it will generate a StackOverflowError. Because we’re trying to write bulletproof programs, this isn’t good.

What’s next

Now that we looked at (a) basic recursion with the sum function, (b) how that works with stacks and stack frames in the last two lessons, and (c) how basic recursion can throw a StackOverflowError with large data sets, the next lesson shows how to fix these problems with something called “tail recursion.”

See also

I didn’t get into all of the nitty-gritty details about the stack and stack frames in this lesson. If you want to learn more about the stack, here are some excellent resources:

• Chapter 5 of Inside the Java Virtual Machine, by Bill Venners is an excellent resource. You may not need to read anything more than the content at this URL.
• Chapter 2 of Oracle’s JVM Specification is also an excellent resource.
• This article titled, Understanding JVM Internals on cubrid.org is another good read.
• If you want even more gory details, an article titled, Understanding the Stack on umd.edu is excellent.
• Here’s an article I wrote about the differences between the stack and the heap a long time ago.