Another way to view recursion is with visual diagrams. To demonstrate this, I’ll use this rectangular symbol in this lesson to represent a function:
The first step
Using that symbol and a list with only three elements, the first sum function call looks like this:
The top cell in the rectangle indicates that this first instance of sum is called with the parameters 1,2,3. Note that I’m leaving the “List” name off of these diagrams to make them more readable.
The body of the function is shown in the middle region of the symbol, and it’s shown as return 1 + sum(2,3). As I mentioned before, you don’t normally use the return keyword with Scala/FP functions, but in this case it makes the diagram more clear.
In the bottom region of the symbol I’ve left room for the final return value of the function. At this time we don’t know what the function will return, so for now I just leave that spot empty.
The next steps
For the next step of the diagram, assume that the first sum function call receives the parameter list (1,2,3), and and its body now calls a new instance of sum with the input parameter sum(2,3) (or sum(List(2,3)), if you prefer). You can imagine the second case expression separating the List into head and tail elements:
Then this sum instance makes a recursive call to another sum instance:
Again I leave the return value of this function empty because I don’t know what it will be until its sum call returns.
It’s important to be clear that these two function calls are completely different instances of sum. They have their own input parameter lists, local variables, and return values. It’s just as if you had two different functions, one named sum3elements and one named sum2elements:
Just as the variables inside of sum3elements and sum2elements have completely different scope, the variables in two different instances of sum also have completely different scope.
Getting back to the sum example, you can now imagine that the next step will proceed just like the previous one:
The last recursive sum call
Now we’re at the point where we make the last recursive call to sum. In this case, because 3 was the last integer in the list, a new instance of sum is called with the Nil value:
With this last sum call, the Nil input parameter matches the first case expression, and that expression simply returns 0. So now we can fill in the return value for this function:
Now this sum instance returns 0 back to the previous sum instance:
The result of this function call is 3 + 0 (which is 3), so you can fill in its return value, and then flow it back to the previous sum call:
The result of this function call is 2 + 3 (5), so that result can flow back to the previous function call:
Finally, the result of this sum instance is 1 + 5 (6). This was the first sum function call, so it returns the value 6 back to whoever called it:
| this post is sponsored by my books: | |||
#1 New Release |
FP Best Seller |
Learn Scala 3 |
Learn FP Fast |
Other visualizations
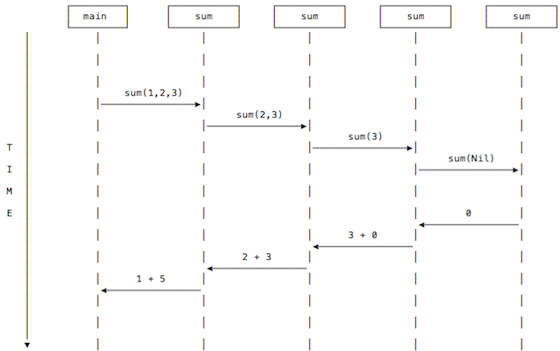
There are other ways to draw recursive function calls. Another nice approach is to use a modified version of a UML “Sequence Diagram.” Note that in this diagram “time” flows from the top to the bottom:
This diagram shows that the main method calls sum with the parameter List(1,2,3), where I again leave off the List part; it calls sum(2,3), and so on, until the Nil case is reached, at which point the return values flow back from right to left, eventually returning 6 back to the main method.
You can write the return values like that, or with some form of the function’s equation, like this:
Personally, I use whatever diagram seems to help the most.
Summary
Those are some visual examples of how recursive function calls work. If you find yourself struggling to understand how recursion works, I hope these diagrams are helpful.